

Figure 1. Différentes forces s'opposent à l'avancement du cycliste.
En cyclisme, différentes forces s'opposent à l'avancement du cycliste et de sa bicyclette et limitent sa vitesse de déplacement. À vitesse élevée (> 40 km·h-1), la traînée aérodynamique est la plus importante de toutes ces forces.41 Pour se représenter son importance, il faut savoir que 90% de la puissance produite par un cycliste sert à vaincre cette résistance. 7,16,38,41 L'aérodynamisme est une problématique de premier plan pour la recherche en cyclisme, l'objectif principal étant d'améliorer les performances.
Durant les courses cyclistes, et plus particulièrement lors des épreuves de "Contre-la-montre", les différences de temps entre les athlètes peuvent être minimes. L'optimisation des paramètres aérodynamiques du cycliste et de sa bicyclette peuvent être déterminants pour augmenter la vitesse de déplacement pour une même production de puissance. Or, pour minimiser la résistance aérodynamique, il est important de connaître ses paramètres déterminants, de savoir comment les évaluer et de pouvoir déterminer leur évolution en fonction de la position du cycliste et de sa vitesse de déplacement.
Ce dossier a pour but de vous présenter les différentes méthodes de terrain et de laboratoire disponibles actuellement pour l'évaluation de la traînée aérodynamique et de son paramètre essentiel : l'aire frontale effective afin d'améliorer la performance en cyclisme.
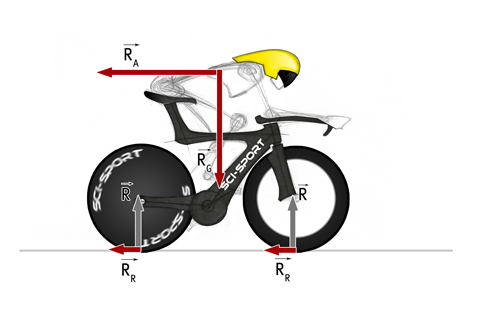
Figure 2. Ensemble des forces opposées à l'avancement du cycliste... (Cliquez sur l'image pour l'agrandir)
Mais tout d'abord, afin de mieux comprendre l'intérêt et l'utilisation de ces méthodes, nous allons faire le point sur les différentes forces qui s'opposent à l'avancement de l'ensemble cycliste-bicyclette. Elles sont au nombre de 3 et sont présentées par ordre décroissant d'importance :
La résistance due à la gravité (RG, en N) représente la force exercée par la masse de l'ensemble cycliste-bicyclette (M, en kg) et orientée verticalement vers le bas. Sur terrain plat, cette force est nulle. Mais sur terrain incliné, c'est la principale résistance de la performance en montée. Elle est donc dépendante de la masse du cycliste, de celle de son vélo et de l'inclinaison du terrain (θ, en degrés). Elle se détermine ainsi, avec l'accélération gravitationnelle (g = 9.81 m·s-2) :
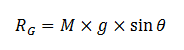

Sur les panneaux routiers, l'inclinaison d'une pente est indiquée en pourcentage et non pas en degrés. Une pente de 10%, par exemple, correspond à un déplacement horizontal de 100m et à un déplacement vertical de 10m, et 10m représente bien 10% de 100m.
Pour déterminer l'angle d'inclinaison de la pente correspondant, vous devez utiliser la fonction trigonométrique tangente :
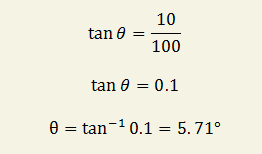
Ces résistances représentent principalement le contact des roues avec le terrain sur lequel évolue le cycliste et les frictions pièces mécaniques entre elles (e.g., transmission par chaîne, etc.).
Les pertes de puissance liées à la transmission par chaîne représente environ 3-5% de la production de puissance totale.41
En cyclisme, à des vitesses de déplacement supérieures à 40 km·h-1, la résistance de roulement (RR, en N) représente environ 10% des résistances totales à l'avancement (RT, en N). Néanmoins, à des vitesses plus faibles (~ 25 km·h-1), RR peut représenter environ 30% de RT. Pour des vitesses inférieures à 100 km·h-1, RR est indépendante de la vitesse de déplacement.41 On peut exprimer RR de la manière suivante :
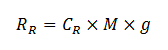
Le coefficient de roulement, et d’une manière générale RR, dépend essentiellement de la pression de gonflage des pneumatiques (PR, en kPa), des matériaux composant les pneumatiques, de la nature du terrain (i.e., enrobé, terre, pavé, herbe, asphalte, piste synthétique, etc.) et du poids de l'ensemble cycliste-bicyclette. D'après Grappe et al.28, CR peut être exprimé en fonction de PR comme suit (Fig. 2) :
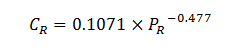
Cette relation montre que plus les pneumatiques seront gonflés et plus le coefficient de roulement, et donc la résistance de roulement sera faible. Prenons un exemple concret : sur une piste au niveau de la mer (altitude = 0m), un cycliste réalise le record de l'heure. Il a 1 heure pour parcourir la plus grande distance possible. L'ensemble cycliste-bicyclette pèse 80kg et le cycliste produit une puissance moyenne de 450 Watts :
Soit un gain d'1 km·h-1 entre une pression de gonflage de 300 et 600 kPa et un gain de 0.75 km·h-1 entre une pression de gonflage de 600 et 1200 kPa. Dans le cadre d'un record de l'heure, la distance de 750 m est assez significative.
Cette résistance est composée de 2 forces : la force de traînée et la force de portance (Fig. 4). En cyclisme, au vu des vitesses de déplacement, la portance est considérée comme négligeable. Dans ce dossier, la résistance aérodynamique sera donc assimilée à la traînée.
Comme cela a été dit dans l'introduction, à grande vitesse, la résistance aérodynamque représente environ 90% des résistances totales opposées à l'avancement d'un cycliste et de sa bicyclette. Elle représente la résistance de l'air à notre déplacement. Plus un cycliste se déplacera rapidement et plus il rencontrera de résistances. Ainsi, pour une production de puissance constante, si on peut diminuer la résistance aérodynamique, la vitesse de déplacement augmente.
La résistance aérodynamique est directement proportionnelle à l'aire frontale projetée du cycliste et de sa bicyclette (Ap, en m2), au coefficient de traînée (CD, sans unité), à la masse volumique de l'air (ρ, en kg·m-3) et au carré de la vitesse d'écoulement du fluide sur le corps du cycliste (vf, en m·s-1)17 :
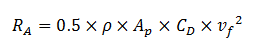
Dans le cas du cyclisme, le fluide dont nous parlerons est l'air. Lorsque le cycliste se déplace, l'air circule à la surface de son corps et de sa bicyclette en sens inverse à celui du déplacement. Plus la vitesse du cycliste augmente, plus l'air circule rapidement et plus la traînée aérodynamique augmente. Cela obligera le cycliste à développer une puissance plus importante.
Lorsque le vent souffle dans le dos du cycliste, celui-ci aura l'impression d'avancer plus rapidement ou tout du moins avec plus de facilité. En effet, le vent qui souffle dans le sens opposé au déplacement des molécules d'air sur le corps permettra de diminuer la vitesse d'écoulement du fluide sur le corps (vf) et donc de diminuer la résistance aérodynamique (Fig. 5).
Inversement, si le vent souffle face au cycliste, celui-ci se sentira freiné. Dans ce cas, le vent augmente la vitesse de déplacement du fluide sur le corps du cycliste. Il en résulte une augmentation de la résistance aérodynamique (Fig. 6).
Pour une vitesse donnée, la traînée aérodynamique est en partie dépendante de la masse volumique de l'air (ρ, en kg·m-3). La masse volumique de l'air est directement proportionnelle à la pression barométrique du fluide (PB, en mmHg) et inversement proportionnelle à la température absolue (T, en K), où la masse volumique de l'airà 760 mmHg et 273K est ρ0 et est égale à 1.293 kg·m-3 :15
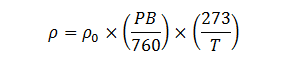

Le kelvin est une mesure absolue de la température, c'est-à-dire qu'il n'y a pas de valeurs négatives. La température 0 K est égale à -273.15°c, c'est le zéro absolu.
La masse volumique de l'air est affectée par l'humidité mais cet effet est faible et peut être négligé.16 De plus, pour une température donnée, la pression barométrique d'un fluide diminue avec l'altitude au-dessus du niveau de la mer (Table 1). Pour T = 273 K, la diminution de PB avec l'altitude (Alt, en km) peut être décrite par la relation suivante :16
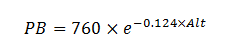
Pour des paramètres identiques, l'augmentation de l'altitude de 0 à 2250m (Mexico, Mexique) permet une diminution de RA d'environ 24% (Table 1).
| Table 1. Influence de la masse volumique de l'air sur la traînée aérodynamique. | ||||
|---|---|---|---|---|
| Piste | Alt (km) | PB (mmHg) | ρ (kg·m-3) | RA (N) |
|
a À une température de 20°c. b Basée sur l'équation de la résistance aérodynamique pour un cycliste avec ApCD = 0.221 m2 et vf = 15 m·s-1. Alt : Altitude; PB : Pression barométrique; ρ : Masse volumique de l'air; RA : Traînée aérodynamique; Ap : Aire frontale projetée; CD : Coefficient de traînée; vf : Vitesse d'écoulement du fluide sur le corps du cycliste |
||||
| Bordeaux (France) | 0 | 760 | 1.20 | 29.8 |
| Colorado Springs (CO, Etats-Unis) | 1.84 | 605 | 0.96 | 23.9 |
| Mexico (Mexique) | 2.25 | 575 | 0.91 | 22.6 |

Figure 7. Aire frontale projetée d'un cycliste (en noir).
L'aire frontale projetée représente la portion du corps qui peut être vue par un observateur placé exactement en face de ce corps (Fig. 7). Elle est dépendante de la taille et de la masse corporelle du cycliste, de la position du cycliste sur la bicyclette et de l'équipement utilisé (e.g., casque, forme du cadre, vêtements).
Certains auteurs ont supposé que Ap était une fraction constante de la surface corporelle totale (ASCT, en m2) (i.e., la surface de peau du corps entier). Cette supposition leur a permis d'établir de manière assez simple des descriptions mathématiques de la traînée aérodynamique 8,17,47,48 puisque ASCT peut être facilement estimée grâce à deux paramètres anthropométriques : la taille (h, en cm) et la masse coporelle (mc, en kg) :19,52
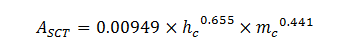
Cependant, Swain et al. (1987) et Garcia-Lopez et al. (2008) ont montré que Ap n'était pas proportionnelle à ASCT car le rapport ASCT / mc tend à être plus petit chez les grands cyclistes. Heil (2001) a néanmoins montré que cette supposition semblait correcte pour les cyclistes dont la masse corporelle se situait entre 60 et 80kg.
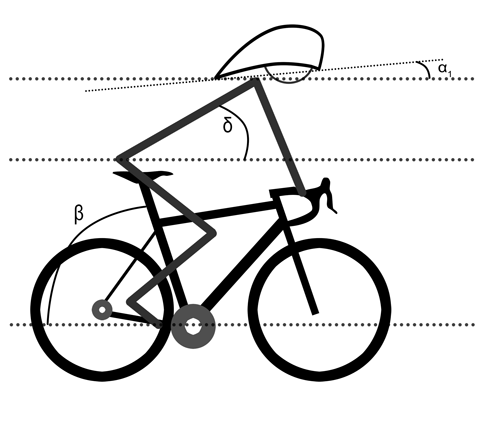
Figure 8. Angles de positionnement du cycliste sur sa bicyclette : β, angle du tube de selle; δ, angle du tronc; α1, angle d'inclinaison du casque.
L'aire frontale projetée peut aussi être exprimée en fonction de la position du cycliste sur sa bicyclette en utilisant l'inclinaison du tube de selle (β, en degrés), l'inclinaison du tronc du cycliste par rapport à l'horizontal (δ, en degrés) (Fig. 8) :30,31
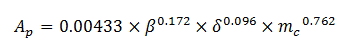
Toutefois, Garcia-Lopez et al. (2008) ont observé une faible corrélation entre l'angle du tronc et l'aire frontale projetée (r = 0.42, p < 0.05). Faria et al. (2005) ont proposé une formule pour déterminer Ap en position dite aérodynamique avec un guidon équipé de prolongateurs en utilisant mc et hc :
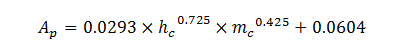
En 2010, Barelle et al. ont établi 2 modèles pour déterminer Ap dans la position aérodynamique avec un guidon équipé de prolongateurs et un casque de Contre-la-montre. Leurs modèles sont fonction de hc, de mc, de la longueur du casque (L, en m) et de son inclinaison par rapport à l'horizontal (α1, en degrés) (Fig. 8) :
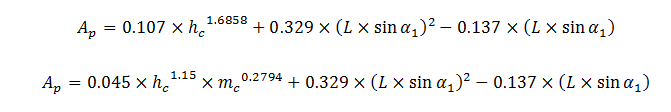
Ces formules sont utiles dans la mesure où elles permettent une estimation rapide de Ap en fonction de quelques valeurs simples à obtenir. Néanmoins, cette estimation reste très peu fiable, les formules ne sont pas toujours standardisées pour une position particulière. Et comme nous allons le voir dans les chapitres suivants, les méthodes pour mesurer directement l'aire frontale projetée sont nombreuses, de telles formules perdent donc leur intérêt.
Enfin, il faut garder à l'esprit que l'aire frontale projetée donne une mesure dans un seul plan de l'espace. Or, le corps en déplacement est tridimensionnel. La mesure seule de Ap permet une estimation de la position adoptée sur la bicyclette par le cycliste. De plus, la mesure d'Ap donne la possibilité d'isoler CD et ainsi d'obtenir des informations sur son évolution selon différents paramètres.
Le coefficient de traînée (CD, sans unité) (également appelé coefficient de forme ou CX) est utilisé pour modéliser les facteurs complexes de forme, de position et les flux d'air agissant sur le corps du cycliste en déplacement. CD est le rapport entre RA et le produit de la pression dynamique (q, en Pa) du fluide en mouvement et Ap :51
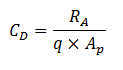
Où la pression dynamique est l'équivalent de l'énergie cinétique par unité de volume d'un corps solide en mouvement. Elle représente la pression de l'air en mouvementest sur le corps du cycliste et elle est définie par l'équation suivante :
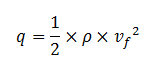
CD est dépendant du nombre de Reynolds (Re). Re est un nombre sans unité qui donne une mesure du ratio des forces inertielles sur les forces visqueuses. Donc pour résumer, CD dépend de la vitesse de l’air et de la rugosité de la surface du corps en mouvement. Ainsi, pour une position donnée sur une bicyclette, l’évolution de la relation entre RA et la vitesse relative au fluide n’est pas linéaire.
Les Figures 12 à 17 (ci-dessous) illustrent les différents recordmen du Record de l'heure au cours du temps et les différentes positions adoptées. Les photographies sont classées par CD décroissant. Il faut toutefois retenir que la position très aérodynamique d'Obree ne lui permettait pas de produire une grande puissance. Sur ces 6 exemples, c'est Boardmann, en 1996, qui a trouvé le meilleur compromis aérodynamisme-production de puissance avec sa position "Superman".

Figure 12. Merckx (1972) - CD = 0.75.

Figure 13. Indurain (1994) - CD = 0.65.

Figure 14. Rominger (1994) - CD = 0.60.

Figure 15. Boardmann (1996) - CD = 0.55.

Figure 16. Obree (1994) - CD = 0.50.

Figure 17. Varna Diablo II (V.P.H.) - CD = 0.097.
Lors de recherches récentes en soufflerie, Grappe (2009) a montré que la relation entre l’aire frontale effective (ApCD, m2) et la vitesse de l’air était hyperbolique (Fig. 18). Les mesures ont été réalisées avec un cycliste de haut-niveau sur une bicyclette de route traditionnelle en position traditionnelle aérodynamique (TAP), où le tronc est parallèle au sol, avec les mains positionnées sur la partie basse du guidon et avec les coudes fléchis à 90°. Ces données indiquent que ApCD diminue entre 4,2 et 11,1 m·s-1, et augmente entre 11,1 et 13,9 m·s-1.
Mais pour 3 cyclistes avec des bicyclettes de piste en position de compétition (DP), où le tronc est partiellement parallèle au sol, avec les mains en bas du guidon et les coudes en extension complète, ApCD diminue entre 5,6 et 19,4 ms-1 (Fig. 19). La position et la vitesse de l’air pourraient avoir un effet significatif sur Re.
Oggiano et al. (2009) ont observé en soufflerie que RA était également dépendante de la vitesse et de la rugosité du textile porté. La conclusion a mis en lumière le fait qu’utiliser un tissu avec une plus grande rugosité peut permettre une réduction de la traînée aérodynamique à des vitesses de déplacement faible, tandis qu’un tissu moins rugueux permettra un meilleur gain à grande vitesse.
En 2009, Grappe a également étudié l’effet de la rugosité sur ApCD en conditions réelles. Sur un vélodrome, la puissance mécanique produite d’un cycliste sur une bicyclette de piste a été mesurée à l’aide d’un wattmètre SRM en position TAP. La puissance produite par le cycliste a été comparée à différentes vitesse entre 8,7 et 13,9 m·s-1 dans deux conditions : 1) avec le système cycliste – bicyclette couvert d’un produit spécial censé amélioré la rugosité ; et 2) sans aucun traitement (Fig. 20).
Entre 11 et 12 m·s-1, il n’existe aucune différence entre les deux conditions expérimentales. Entre 8,7 et 11 m·s-1, le traitement de surface permet une augmentation de la vitesse du système cycliste – bicyclette pour la même puissance mécanique produite. Cependant, pour des vitesses de déplacement plus grandes que 12 m·s-1, la vitesse n’augmente pas dans la condition où le traitement est appliqué.
Ces résultats montrent toute la complexité de la relation entre CD, la vitesse du fluide sur le corps en déplacement et la rugosité de la surface. Des études plus avancées devront être menées pour mieux comprendre l’évolution de CD en fonction de la vitesse de déplacement, de l’anthropométrie du cycliste, de sa position, et du type de vêtements qu’ils portent.
Pour une vitesse donnée, l’aire frontale effective (ApCD, en m2) est le paramètre le plus important de la traînée aérodynamique. En estimant ApCD, il est possible d’évaluer le profil aérodynamique et la position optimale sur la bicyclette diminuant RA. L’estimation de ApCD permet d’évaluer l’aérodynamisme d'une position et de l’équipement,21 dans le but de les optimiser (Fig. 21). Cette estimation offre la possibilité d’établir des modèles mathématiques pour prédire la performance.
Pour une condition climatique particulière et pour une vitesse donnée, les paramètres sur lesquels il est possible d'avoir le plus d'influence sont l'Ap et le CD. En les évaluant, il est possible de quantifier le profil aérodynamique d'un cycliste et de déterminer la position optimale sur la bicyclette. Ce chapitre présente les différentes méthodes existantes pour déterminer ces variables.
La soufflerie est la méthode de référence pour déterminer l'aire frontale effective.34 Un flux d'air est artificiellement généré sur l'ensemble cycliste-bicyclette et la mesure de la traînée aérodynamique se base sur la quantification des forces de réaction au sol. En fait, le cycliste et sa bicyclette sont placés sur une plateforme de force (Fig. 22), lorsque le flux d'air passe sur le cycliste, il rencontre une résistance et la plateforme de force est suffisamment sensible pour mesurer cette résistance, la traînée aérodynamique, et il est ainsi possible de déterminer ApCD :
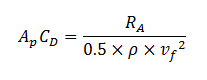
Cette technique est si sensible qu'elle permet de mesurer l'aire frontale effective selon le type de roue,54 l'orientation du vélo par rapport au flux d'air,39 et la position du cycliste. 22,23 Bien qu'étant la méthode de référence dans l'analyse de l'aérodynamisme, elle reste très chère (entre 5000 et 10000 euros / jour) et peu d'études publient les données obtenues. Voici les différentes limitations de cette technique :
Cette méthode est dite "de terrain" car elle permet une estimation de la traînée aérodynamique et de la résistance de roulement en conditions réelles. Comme je vous l'ai expliqué au début de ce dossier, en cyclisme, sur terrain plat, la résistance totale à l'avancement est composée principalement de deux forces : la traînée aérodynamique et la résistance de roulement. Cela peut être exprimé ainsi :8,10,17, 27,28
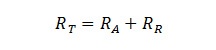
Et donc :
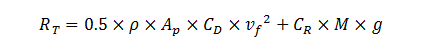
Les forces totales opposées à l'avancement peuvent être déterminées en mesurant la production de puissance mécanique en fonction de la vitesse de déplacement :27
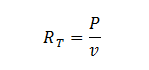
L'analyse par régression linéaire consiste à mesurer la puissance produite à l'aide d'un wattmètre (e.g., SRM ou PowerTap) à différentes vitesses pour déterminer les résistances totales à l'avancement. Pour cela, le cycliste réalise plusieurs essais à différentes vitesses dans une position définie. En obtenant la puissance produite à chaque vitesse, il est possible de créer un nuage de points représentant RT en fonction de la vitesse au carré (Fig. 23).
A partir de ce graphique, une régression linéaire est effectuée. L'équation de cette droite est de la forme y = ax + b. Or, RT peut s'exprimer en fonction de la vitesse de la manière suivante :
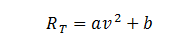
Par analogie :
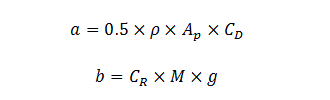
Grâce à cette méthode, il est possible d'estimer l'aire frontale effective pour une position donnée à partir de la pente de la droite de régression linéaire (i.e., a), ainsi que le coefficient de roulement (grâce à b), ce qui permettra d'analyser la résistance de roulement en fonction du terrain. Cette méthode est très fiable et elle est plus ou moins sensible selon le wattmètre utilisé. En utilisant un pédalier SRM, il est fort probable de réussir à différencier l'aérodynamisme de différentes positions presque identiques. C'est l'une des méthodes les plus utilisées.
Cette méthode consiste à mesurer les forces de traction en remorquant un cycliste sur sa bicyclette avec un véhicule motorisé (e.g., voiture, scooter, etc.) au moyen d'un câble sur une piste plate à vitesse constante. La longueur du câble doit être suffisamment grande pour minimiser les turbulences causées par le véhicule remorqueur. 7,28 Durant les essais, le cycliste doit toujours garder la même position sur sa bicyclette. De plus, il peut pédaler à vide pour induire les turbulences aérodynamiques provoquées par le pédalage.8
Les résistances totales à l'avancement sont mesurées grâce à un capteur de force sur lequel est attaché le câble. Ainsi la résistance qu'oppose l'ensemble cycliste-bicyclette est mesurée. Comme pour la méthode d'analyse par régression linéaire, il est nécessaire de réaliser plusieurs essais à différentes vitesses pour obtenir une courbe décrivant RT en fonction de v2, puis d'obtenir l'équation de la droite de régression linéaire et ainsi connaître ApCD et CR.
Cette méthode est aujourd'hui très peu utilisée et les limites de mesure (e.g., turbulences provoquées par le véhicule remorqueur) ne font pas d'elle la méthode la plus pertinente. Depuis l'arrivée de wattmètres abordables sur le marché, il est conseillé d'utiliser l'analyse par régression linéaire.
Ces méthodes de mesure de la traînée aérodynamique sont basées sur la seconde loi de Newton (i.e., ΣF = m × a), où la somme des forces résistives est égale au produit de l'accélération et de la masse. Elles consistent à mesurer l'accélération ou la décélération d'un cycliste dans une position définie à l'aide de cellules photoélectriques. Le cycliste réalise plusieurs passages à différentes vitesses. Grâce à ces mesures, il est possible de déterminer la résistance aérodynamique et la résistance de roulement.
Dans les deux méthodes, le cycliste doit entrer dans le passage de mesure à une certaine vitesse, puis s'arrêter de pédaler pour ainsi déterminer l'influence des résistances sur son déplacement. La méthode d'accélération était réalisée sur un terrain en pente, mais les variations de mesure étaient de l'ordre de 10%. 37 Tandis que Candau et al. (1999) ont montré que la sensibilité et la reproductibilité de la méthode de décélération (qui se déroule sur terrain plat) étaient excellentes en comparaison à des mesures réalisées en soufflerie.
L'inconvénient majeur de ces méthodes est le lourd protocole à mettre en place. Là où quelques essais à différentes vitesses suffiraient avec la méthode d'analyse par régression linéraire, la méthode de décélération nécessite une vingtaine d'essais.
Parmi ces quatre méthodes, la soufflerie et la méthode d'analyse par régression linéaire sont les plus sensibles et reproductibles. Elles permettent des mesures fiables (plus ou moins selon le modèle de wattmètre choisi pour l'analyse par régression linéaire) représentatives des conditions de terrain. De plus, elles ont l'avantage de pouvoir distinguer l'aire frontale effective de différentes positions du cycliste, avec un avantage pour la soufflerie qui permet d'évaluer un changement de casque ou de petites variations de positions.3,14
Enfin, nous n'avons pas parlé d'une méthode qui commence à être de plus en plus utilisée en cyclisme, mais également en natation, la mécanique des fluides numérique. Defraeye et al. (2010) ont montré que cette méthode numérique de calcul de la dynamique des fluides permettait d'obtenir des traînées aérodynamiques en accord avec celles mesurées en soufflerie. Elle permettra sûrement dans un futur proche d'étudier avec fiabilité et précision le comportement de l'air autour du corps du cycliste en mouvement...
Bien que l'aire frontale effective (i.e., ApCD) soit le principal paramètre dans l'évaluation de l'aérodynamisme, elle est en partie influencée par l'aire frontale projetée (i.e., Ap), une diminution de Ap engendre généralement une diminution de ApCD.14 Et Ap reste une variable facilement quantifiable et donc très utile pour les entraîneurs et les cyclistes pour des évaluations empiriques et un suivi à l'entraînement.
Il est possible de classer les méthodes d'évaluation de l'aire frontale projetée dans deux catégories : 1) celles utilisant une aire d'étalonnage placée à côté du cycliste comme la méthode de pesage des photographies,8,9,12, 17,30,47,48, 49,50,51,53 la méthode de digitalisation3,12,18, 30,31 et 2) celles n'en utilisant pas comme la planimétrie 18,46 et la méthode basée sur l'utilisation d'un logiciel de C.A.O..12
Cette méthode consiste à prendre une photographie du cycliste, de sa bicyclette et d'une zone d'étalonnage dont l'aire est connue dans le plan frontal (Fig. 24). La photographie est développée sur papier puis découpée. Il faut en fait découper 2 parties : la zone d'étalonnage et le corps du cycliste (Fig. 25). Ces deux parties sont ensuites pesées à l'aide d'une balance dont la sensibilité est plus ou moins de 0.001g (Fig. 26).

Figure 24. Photographie dans le plan frontal d'un cycliste, de sa bicyclette et d'une zone d'étalonnage dont l'aire est connue.

Figure 25. La photographie est ensuite développée et les zones représentant le corps du cycliste et la zone d'étalonnage sont découpées.

Figure 26. Les deux zones découpées sont pesées à l'aide d'une balance Metler Toledo AB 204 (± 0,001 gr de sensibilité).
En procédant de la sorte, nous obtenons deux valeurs en grammes. Il suffit ensuite de calculer le ratio entre la masse de l'image du corps et la masse de la zone d'étalonnage puis de multiplier ce ratio par l'aire de la zone d'étalonnage connue pour obtenir l'Ap en m2.

Prenons l'exemple des photographies ci-dessus. Lorsque vous pesez vos deux zones séparément, vous obtenez deux valeurs en grammes.
La zone d'étalonnage pèse environ 0.047 g et la partie représentant le corps du cycliste pèse environ 0.184 g. Et sachant que la zone d'étalonnage a une aire de 0.110148 m2, il est possible de connaître l'aire frontale projetée du corps du cycliste de la manière suivante :

Bien qu'elle soit très rudimentaire, la méthode de pesage des photographies est très utilisée et depuis plusieurs dizaines d'années.9,12,30,48,49,50,51,53 Il faut dire qu'elle nécessite uniquement un appareil photographique, une zone plane dont il faudra calculer l'aire, une balance à haute sensibilité (c'est peut-être le plus difficile à trouver) et un objet tranchant (e.g., couteau de modéliste, cutter, etc.). Cette méthode reste très fiable et elle a permis de valider de nouvelles méthodes qui sont décrites ci-dessous.12,30
Cette méthode présente néanmoins quelques inconvénients qui peuvent être résolus.9,12 Pour une mesure correcte, le découpage doit être précis, et c'est une opération assez fastidieuse qui peut prendre entre 5 et 6 minutes par photographie. De plus, la taille d'impression standard des photographies ne permet pas de découper avec une précision suffisante la bicyclette. La mesure de l'aire frontale projetée est donc limitée à celle du corps du cycliste (l'aire frontale d'une bicyclette de route classique est généralement de 0.11 m2). Pour contourner ce problème, il suffirait d'imprimer les photographies dans un plus grand format.
Sur le principe, cette méthode est identique à la méthode de pesage des photographies. Il est nécessaire de prendre une photographie du cycliste sur sa bicyclette et d'une zone d'étalonnage placée sur le côté (Fig. 27). Cependant la différence réside dans le traitement de l'image. Ici, plus besoin de développer les photographies, tout est numérique. Des logiciels gratuits (e.g., ImageJ) permettent de déterminer le nombre de pixels que contient une zone délimitée. Il est possible de connaître le nombre de pixels présents dans la zone d'étalonnage et dans la zone correspondant au cycliste et à sa bicyclette (Fig. 28), et ainsi, de connaître l'aire frontale projetée du cycliste et de sa bicyclette.3,12,18,30,31

Figure 27. Photographie d'un cycliste.

Figure 28. Image traitée dans ImageJ.
La méthode de digitalisation est très simple d'utilisation et très rapide. L'inconvénient mineur est la préparation de la photographie à l'aide de logiciels de retouche d'images (e.g., Gimp). Il est souvent impératif de tracer le contour des zones à étudier et de les noircir. Cela requiert un peu de temps et de pratique, mais une fois l'habitude prise, c'est une opération qui est très rapide.
À l'inverse de la méthode de pesage des photographies, il est possible d'obtenir les aires frontales projetées du cycliste et de sa bicyclette et du cycliste seul. Au niveau matériel, cette méthode nécessite un ordinateur personnel, le logiciel ImageJ (gratuit), un appareil photographie numérique et un logiciel de retouche d'image (Gimp est gratuit). Enfin, cette méthode est valide en comparaison à la méthode de pesage des photographies.12,30
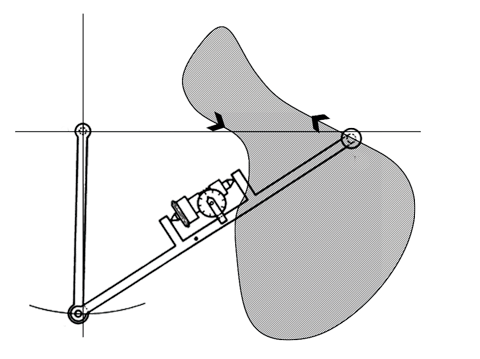
Figure 29. Planimètre.
Avec cette méthode, le contour d'un cycliste et de sa bicyclette est tracé à l'aide d'un planimètre (Fig. 29), et l'aire délimitée est déterminée par triangulation.46 Pour de plus amples explications sur le principe de fonctionnement d'un planimètre, je vous conseille ce lien en anglais.
Le principal avantage de cette méthode est qu'elle ne nécessite pas de zone d'étalonnage placée à côté du cycliste. Cela permettrait donc de prendre des photographies en situation de course et de les analyses ensuite. Cependant, Olds & Olive (1999) ont comparé cette méthode à la méthode de pesage de photographies, et il s'avère que la méthode de pesage des photographies soit plus fiable.
Comme pour la méthode de digitalisation, cette méthode ne requiert pas de zone d'étalonnage à placer à côté du cycliste. Elle peut donc servir à analyser des aires frontales projetées à partir de photographies prises en conditions réelles.
Cette méthode consiste à déterminer l'aire frontale projetée à l'aide d'un logiciel de C.A.O.. Pour cela, il faut ouvrir la photographie dans le logiciel et la remettre à l'échelle 1:1. Il suffit de prendre une référence verticale ou horizontale (e.g., la largeur du guidon ou la hauteur de la roue avant) (Fig. 30). Puis, le contour à mesurer est détourer à l'aide d'un outil de type courbes de Béziers (Fig. 30). Enfin, il suffit de créer un volume tridimensionnel à partir de contour et le logiciel permet de mesurer l'aire frontale projetée (Fig. 30).12
Les mesures sont valides et reproductibles en comparaison à la méthode de pesage des photographies.12 Les mesures de Ap sont rapides et simples, et il est possible de mesurer Ap dans des conditions de terrain. Néanmoins cette méthode nécessite d'avoir à disposition un logiciel de C.A.O..
Parmi les différentes méthodes décrites pour évaluer l'aire frontale projetée, la méthode de digitalisation et la méthode basée sur l'utilisation d'un logiciel de C.A.O. sont les mieux adaptées pour le format numérique. La méthode de pesage des photographies et la planimétrie nécessite une procédure plus fastidieuse et plus longue. Cependant, toutes ces méthodes sont valides et fiables, même si la planimétrie semble moins précise. Les méthodes numériques sont simplement plus simples et plus rapides.12
Néanmoins, toutes ces méthodes ont en commun la prise d'une photographie de l'ensemble cycliste-bicyclette. Puisque la mesure de Ap est directement dépendante de la photographie, le placement de la zone d'étalonnage et de l'appareil photographique peuvent être source d'erreurs. Pour étudier certaines de ces erreurs de mesure, Olds & Olive (1999) ont déterminé les effets sur Ap du positionnement de la zone d'étalonnage et de l'appareil photographique par rapport au cycliste. Voici les recommandations qu'ils préconisent pour prendre des photographies utiles :
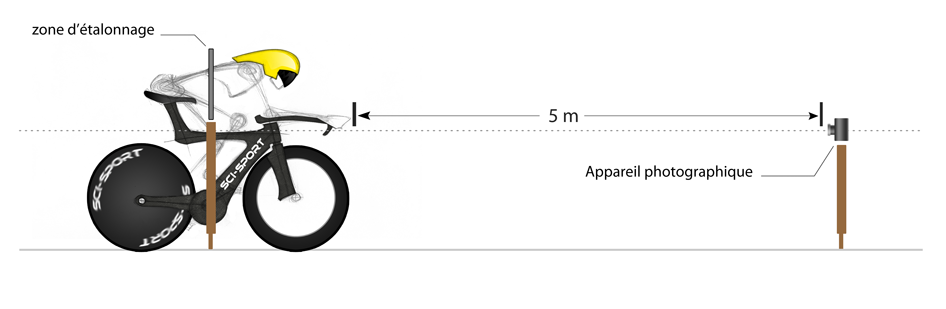
Figure 31. Pour prendre une photographie utile à la mesure de l'aire frontale projetée, il est nécessaire de placer l'appareil photographique dans le prolongement de la bicyclette, à hauteur du guidon et à une distance d'au moins 5 mètres. Et la zone d'étalonnage doit se trouver entre les épaules et les hanches.
En cyclisme, la traînée aérodynamique est composée de 2 formes de traînée : la traînée de pression et la traînée de frottement.21,41 La traînée de pression est la plus importante. Elle représente la différence de pression qui existe entre l'avant et l'arrière du corps du cycliste en mouvement. Dans un fluide, une couche limite se crée sur le corps en mouvement due à la pression du fluide sur ce corps, cela provoque des turbulences à l'arrière résultant en une traînée de pression.41 La traînée de pression est principalement dépendane de la taille générale et de la forme du corps en mouvement. La traînée de frottement est une résistance qui est générée par le contact des molécules du fluide directement sur la surface du corps en mouvement. Cette résistance augmente avec la taille et la rugosité de la surface.41
Comme expliqué précédemment, l'aire frontale effective (ApCD) est le paramètre déterminant l'aérodynamisme de l'ensemble cycliste-bicyclette. À la fois la taille et la forme du corps en mouvement affectent ApCD et peuvent être diminués de plusieurs manières.37,41 Un cycliste peut diminuer RA en réduisant Ap. L'angle entre le tronc et le sol est important, plus cet angle sera proche de 0° plus Ap sera diminuée.30. Faria (1992) ont rapporté une diminution de 20% de RA lorsque les coudes du cyclistes sont pliés avec le buste presque à la parallèle avec le sol.
La position des bras est un facteur supplémentaire à modifier dans le but d'améliorer Ap. Une diminution de 28% de RA est observée lorsque les mains sont placées au centre du guidon avec le buste reposant sur les mains, et les manivelles parallèles au sol.21 Les mains peuvent être placées plus en avant encore en utilisant des prolongateurs (comme sur lors des Contre-la-montre), cela augmente le confort et diminue Ap. De plus, Berry et al. (1994) n'ont pas trouvé de différences significatives entre les guidons avec prolongateurs et les guidons standards en terme de fatigue, de production de puissance ou de consommation d'oxygène.

Figure 32. Comment minimiser la traînée aérodynamique en cyclisme ?
Les effets de la forme de l'ensemble cycliste-bicyclette sur RA sont quantifiés par le coefficient de traînée (CD).15 Pour réduire CD, le corps et la bicyclette doivent être profilés. La position, le cadre, le casque, les roues, les vêtements et autres accessoires peuvent significativement réduire CD.20,21 Tew & Sayers (1999) ont montré que des roues avec jantes profilées pouvaient réduire la traînée aérodynamique axiale de plus de 50% en comparaison à des roues à rayons classiques.
Jeukendrup et Martin (2001) ont utilisé un modèle avec des facteurs multiples concernant ApCD (e.g., position du corps, cadre de la bicyclette, roues, etc.). Leur modèle a été utile pour montrer la diminution du temps prédit pour parcourir une course contre-la-montre de 40 km en modifiant ces facteurs. Par exemple, la modification de la hauteur du guidon a permis de diminuer l’Ap de 5,8 %, et ce changement s’est traduit pas une diminution du temps sur 40 km de 1 minute. Pour une même position du cycliste, l’utilisation d’un cadre dit aérodynamique a permis de diminuer le temps sur 40 km d’un peu plus que 1 minute en comparaison avec un cadre traditionnel.
Différentes techniques existent pour améliorer ApCD du cycliste et de sa bicyclette et il est possible de régler de nombreux paramètres. Néanmoins, chaque amélioration devra être testée et quantifiée sur le terrain (à l'aide d'une des techniques décrites plus haut) pour voir si la diminution de ApCD ou de Ap peut avoir une influence positive significative sur la performance sur route. De plus, il est très important de trouver pour chaque cycliste le bon compromis entre aérodynamisme, ergonomie et production de puissance.2 En effet, les positions les plus aérodynamiques ne sont pas forcément les positions les plus confortables, et ce que vous gagneriez d'un côté vous ferait peut-être perdre beaucoup de l'autre. Il est donc primordial de tester les positions en laboratoire et sur le terrain, en vérifiant différents paramètres comme la puissance moyenne, la cadence moyenne, etc.
C'est aussi une des raisons pour laquelle les modélisations mathématiques de la performance en cyclisme sont utiles pour simuler la production mécanique de puissance qui est dépendante de nombreux paramètres.
Un modèle théorique peut fournir de nombreuses informations utiles pour les chercheurs, les entraîneurs et les cyclistes eux-mêmes qui n'ont pas forcément accès à tout le matériel nécessaire ou qui veulent simplement estimer et comparer l'effet de différents paramètres sur la performance. Un modèle est censé permettre d'étudier et de prédire les changements physiologiques, biomécaniques, anthropométriques et environnementaux.47 De nombreux auteurs ont établis des modélisations mathématiques de la performance en cyclisme,2,5,17,30,38,42,44,45,47,48,49 la plupart sont dépendants de la puissance produite par le cycliste pour vaincre les résistances à l'avancement.38
Gonzales-Haro et al. (2007, 2008) ont comparé 9 modèles théoriques qui permettaient d'estimer la production de puissance. Les variables les plus importantes dans ces modèles étaient : la vitesse, la masse du cycliste et de sa bicyclette et les variables aérodynamiques (i.e., Ap et CD). Les autres variables secondaires étaient la pente, le coefficient de roulement et les conditions climatiques (Latin) signifie 'c'est à dire'">i.e., pression barométrique et température). L'équipe de scientifiques a trouvé que les équations de di Prampero (1979) et de Candau et al. (1999) permettaient les meilleures estimations de la production de puissance en comparaison avec des mesures réalisées sur le terrain avec un wattmètre SRM.
Pour l'équation de di Prampero (1979), la puissance P est exprimée en Watts, M représente la masse du cycliste et de sa bicyclette en kg, v est la vitesse de déplacement en m·s-1, PB est la pression barométrique en mmHg, T est la température absolue en kelvin et ASCT est la surface cutanée corporelle totale en m2. Elle peut être déterminée à partir de la masse corporelle du cycliste (mc, en kg) et de la taille du cycliste (hc, en m) :
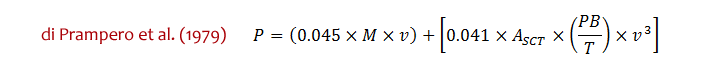
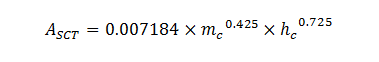
Pour l'équation de Candau et al. (1999), la puissance P est exprimée en Watts, CR représente le coefficient de roulement, M est la masse du cycliste et de sa bicyclette en kg, g est l'accélération gravitationnelle dont la valeur est 9.81 m·s-2, d est la distance de la course en m, t est le temps de la course en s, ρ est la masse volumique en kg·m-3 et ApCD est l'aire frontale effective en m2 :
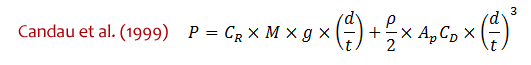
Comme cela a été expliqué dès le début de ce dossier, à des vitesses de déplacement supérieures à 40 km·h-1, 90% de la puissance mécanique est produite pour lutter contre la traînée aérodynamique. Or cette résistance est principalement dépendante de l'aire frontale effective. Il est donc primordial que ApCD soit correctement évaluée pour permettre une simulation théorique plus précise. De nombreuses études ont établi des modélisations de la performance plus ou moins complexes. Le problème majeur, commun à toutes ces publications, était le manque de précision concernant Ap et CD. Au mieux, ApCD était évalué via la soufflerie pour 1 cycliste et le modèle était établi de cette façon, au pire, ApCD était determinéé à partir des paramètres anthropométriques et donc basé sur des estimations d'estimations...
Le modèle mathématique de Candau et al. (1999) se définit, en partie, en fonction de ApCD. En utilisant l'une des techniques présentées plus haut, comme l'analyse par régression linéaire, il est possible d'obtenir une estimation valable de la puissance produite sur un parcours donné.38
L'aire frontale effective est le paramètre le plus important pour caractériser la traînée aérodynamique. Les techniques d'estimation de ApCD sont maintenant bien reconnues en cyclisme, et ce paramètre peut être évalué en laboratoire ou sur le terrain avec une grande fiabilité. Cependant, bien que l'aire frontale projetée soit facilement quantifiable, la variation du coefficient de traînée est plus complexe. Son évolution en fonction de la vitesse de déplacement n'est pas encore totalement maîtrisée. Plus de recherches sont nécessaires pour étudier ses variations, de nouvelles méthodes comme la mécanique des fluides numérique pourrait y aider.
Dans tous les cas, pour optimiser votre performance, il sera presque obligatoire d'estimer ApCD. Pour cela, nous vous conseillons de prendre votre temps et de tester de nombreux paramètres (e.g., différentes positions, différentes roues, différents cadres, etc.). De plus, n'oubliez pas que si l'aérodynamisme est très important, il n'en faut pas moins pédaler, et la position aérodynamique n'est pas toujours la position la plus confortable et donc celle qui permet la production de puissance et la cadence de pédalage optimales. Tout dépendra de la mobilité articulaire et de la souplesse des cyclistes.
Pour plus de précisions ou des conseils personnalisés, n'hésitez pas à nous contacter via notre forum.
Nous vous rappelons que vous pouvez citer les articles sous réserve de limiter votre citation à 200 mots maximum et d'inclure un lien nominatif vers celui-ci. Tout autre utilisation, en particulier la copie en totalité sur un forum de discussions, sur un site internet ou tout autre contenu, est strictement interdite.
Copyright © 2011-2024 - www.sci-sport.com - Tous droits réservés